导读 一个国际研究小组(第一作者是圣彼得堡高等经济学院的 Nikita Kalinin，最后一位作者是墨西哥 CINVESTAV 的 Ernesto Lupercio)提出了

一个国际研究小组(第一作者是圣彼得堡高等经济学院的 Nikita Kalinin，最后一位作者是墨西哥 CINVESTAV 的 Ernesto Lupercio)提出了第一个描述自组织临界性的连续模型。所提出的解决方案比经典的沙堆模型更简单、更通用。它在热带几何背景下整合了经济、发育生物学和重力等相互远离的领域。该论文发表在国家科学院院刊上。

如果外力无论多小，都能产生雪崩效应，导致系统行为发生变化，则称系统处于临界状态。这些包括相变：一旦单个冰晶出现在冷却到零摄氏度的水中，冰团就会立即开始形成。

某些动力系统趋向于临界状态——地震就是一个说明性的例子。虽然水结冰需要一定的温度和压力，但地震发生不需要满足精确的参数。地震的主要原因是构造板块的连续运动，预测系统达到临界状态并产生雪崩的确切时刻几乎是不可能的。

许多研究人员试图解开地震之谜。20 世纪中叶，地震学家古腾堡 (Gutenberg) 和里希特 (Richter) 表明，任何特定地区的地震震级与地震总数之间存在关系。这种关系由幂律描述为双对数刻度上的一条直线。

此后，地球物理学、宇宙学、经济学、风险管理理论和其他领域都发现了具有这一特征的现象。所有这些都可以用自组织临界(SOC)理论来描述。

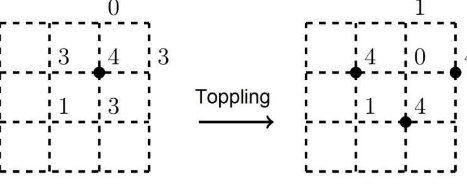
SOC 的概念由 Per Bak、Chao Tang 和 Kurt Wiesenfeld 于 1987 年引入。在他们的开创性论文中，他们提出了 SOC 系统的原型示例：沙堆模型。想象一个方形网格，每个顶点都有沙粒，其中新的沙粒以特定频率落在网格上。假设如果每个顶点的沙粒不超过三个，系统将保持稳定。但是，一旦第四个沙粒落在顶点的顶部，它就会倾倒，沙子从这个峰滑下并重新分配到相邻的顶点。倾覆将继续雪崩，直到系统恢复平衡。物理学家的主要发现是倾倒的顶点数量(即坍塌区域的大小)满足幂律分布。

沙堆模型长期以来一直是描述 SOC 的经典模型。然而，它仅在现象学水平上描述了关键系统的动力学，不能用于模拟地震或预测真实沙堆的行为。

“旧的沙堆模型，纯粹是组合的，与数学的大世界有些不同。我们的模型向前迈进了一步，因为它具有沙堆模型的所有优点，但它也是几何的和连续的，使它更容易使用，”作者、HSE 博弈论与决策国际实验室高级研究员 Nikita Kalinin 解释说。“我们已经证明，在热带几何学的帮助下，可以在不是元胞自动机的连续系统中获得幂律相关性，热带几何学在今天有很多应用。”

CINVESTAV 的 Ernesto Lupercio 博士说：“热带几何是 21 世纪几何学的一个分支，它受到经典代数几何的启发，由于它与许多科学领域(主要是弦论)的联系而蓬勃发展。”

与经典沙堆模型中使用的网格不同，新的热带沙堆模型考虑了一条热带曲线 - 具有直线边缘的平面图 - 被包围在一个正方形中。曲线将正方形划分为多边形区域，每个区域包含一组随机选择的点。当添加一个新点时，热带曲线试图通过它，并且包含该点的多边形区域通过其边缘的平行转移被拉到一起。一旦其中一个边缘到达该点，该过程就会停止。然后添加一个新点，并重新开始。之前的点可能会再次偏离曲线，系统将开始向它移动。

这种收敛过程是将沙粒添加到沙堆的有限变体。在新模型中，雪崩大小对应于通过添加随机点启动的过程中会聚区域扫过的区域。科学家们希望他们的模型将有助于阐明表现 SOC 特性的不同现象之间的关系。

“我们可以通过数学的镜头观察到不同现象的相似之处。热带几何在弦论、经济学和发育生物学中都有应用。我们工作的价值在于在意想不到的地方找到联系。这意味着将方法应用于一个领域可以应用到另一个。你只需要采取下一步，“加里宁说。